Game Theory: Solving Sequential Games

Optimal Sequencing: Utilizing the game tree and backward induction to find the Subgame Perfect Nash Equilibrium.

Happy Wednesday!

Insight Trunk is a free lifetime library—a modern replacement for outdated encyclopedias. From Monday to Saturday, we deliver a 10-minute read on a specific subject, with fresh topics each week. Two years later, we revisit each theme with updated insights from our archives—so you’ll never miss a thing. You can unsubscribe anytime using the link at the bottom of this newsletter.

Today, we shift to analyzing games where players move in turn. We’ll use the Extensive-Form (game tree) and master backward induction to find the robust solution: the Subgame Perfect Nash Equilibrium (SPNE). This method helps eliminate non-credible threats, revealing truly optimal strategies.

🧑‍💻 In this week’s edition: Game Theory

• Monday - Foundations and Representation

• Tuesday - Solving Simultaneous Games

• Wednesday - Solving Sequential Games

• Thursday - Games with Incomplete Information

• Friday - Dynamic and Repeated Games

• Saturday - Key Applications and Concepts

Question of the day

What is the primary solution method used to solve an Extensive-Form game tree?

Let’s find out !

Let’s break it down in today discussion:

• Introducing Extensive-Form Game Trees

• Finding Subgame Perfect Nash Equilibrium (SPNE)

• Using Backward Induction to Solve Games

• Identifying and Avoiding Non-Credible Threats

Read Time : 10 minutes

🌳 Introducing Extensive-Form Game Trees

The analysis of sequential strategic interaction necessitates a specialized framework, which is provided by the Extensive-Form game. This structure visually maps the game’s sequence, information flow, and outcomes using a graphical representation known as the game tree.

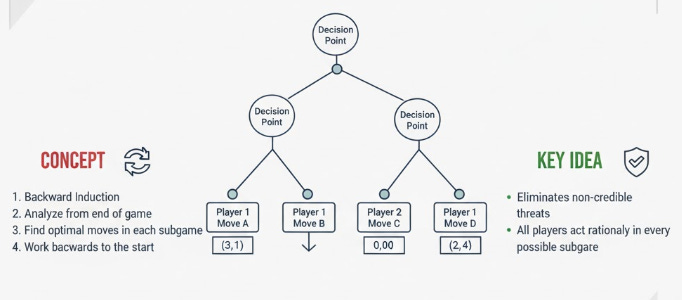
The game tree begins at an initial node (the root) and branches out, with each branch representing a possible action choice. Decision nodes indicate points where a player takes an action, and the specific player moving is clearly identified at that node. This sequential structure is crucial as it formalizes the concept of history—the set of moves made leading up to any given decision point.

The tree’s construction also accounts for information available to players. While typically assumed to be perfect information in simple sequential games (meaning all prior moves are known), the nodes can be grouped into information sets to model imperfect knowledge. The tree terminates at terminal nodes (the leaves), where the final payoffs for all players are explicitly listed, representing the value derived from the sequence of choices made.

This representation is indispensable because it transforms the dynamic nature of sequential interaction into an easily traceable path. By clearly defining who moves when and the subsequent results, the Extensive Form sets the stage for techniques like backward induction, which are required to find credible equilibrium strategies.

✨ Finding Subgame Perfect Nash Equilibrium (SPNE)

In sequential games, the standard Nash Equilibrium (NE) is often insufficient because it can include strategies based on threats that are irrational off the equilibrium path. To ensure robust sequential rationality, the concept of the Subgame Perfect Nash Equilibrium (SPNE) is employed.

An SPNE is a refinement of the Nash Equilibrium. It requires that the players’ strategies constitute a Nash Equilibrium not only for the entire game but also for every subgame of the original game. A subgame is any part of the original Extensive-Form game tree that begins at a single decision node and includes all subsequent moves and payoffs. This criterion forces every decision made by every player to be optimal at the time the decision is made.

The fundamental principle underlying the SPNE is sequential rationality. While an NE only guarantees that players are maximizing their payoffs given the starting strategies of others, the SPNE ensures that players maximize their expected continuation payoff at every stage of the game. This eliminates all equilibria that rely on threats or promises that the player would have no incentive to fulfill once they reach the decision node where the threat must be enacted.

The SPNE is therefore considered the more reliable and robust solution concept for sequential games. By satisfying the best-response condition in every possible subgame, the SPNE identifies a credible equilibrium that reflects optimal planning throughout the entire strategic path .

For an in-depth look, make sure to watch this video.

⬅️ Using Backward Induction to Solve Games

Backward induction is the definitive algorithmic method for identifying the Subgame Perfect Nash Equilibrium (SPNE) in sequential games with perfect information, represented by the Extensive-Form game tree. This technique ensures that every chosen strategy is sequentially rational.

The method mandates working backward from the terminal nodes toward the initial node (the root) of the tree. At the final decision nodes, the player moving at that stage determines their optimal action by simply comparing the immediate payoffs from the available choices. The non-optimal branches leading from that node are effectively pruned, as a rational player will never choose them.

Once the optimal choice is identified at the last stage, the process moves to the preceding set of decision nodes. The player at this earlier stage anticipates the rational, optimal moves of all subsequent players—which have just been determined. They choose the action that maximizes their payoff, taking into account the future actions of the players following them. This means the solution is derived from future consequences impacting present choices.

By repeating this process until the first move, backward induction guarantees that the resulting set of strategies is optimal at every stage of the game. For instance, in an entry game, the incumbent firm decides whether to fight or accommodate based on their anticipation of the entrant’s ultimate rational move, rather than succumbing to a non-credible threat. The strategy profile derived is the unique SPNE .

Broaden your understanding by watching this video.

🔪 Identifying and Avoiding Non-Credible Threats

A critical refinement achieved by using the Subgame Perfect Nash Equilibrium (SPNE) is the systematic elimination of strategies that incorporate non-credible threats. These are threats that, while potentially influential, are irrational for the threatening player to carry out if the threat were ever challenged.

A threat is non-credible if, once the threatened action is reached in the game, the player making the threat would receive a lower payoff by executing the threat than by choosing an alternative, less aggressive action. The standard Nash Equilibrium often includes outcomes sustained by such empty threats because it only requires rationality at the beginning of the game, not throughout every possible decision point.

Backward induction explicitly solves this problem. By starting at the end of the game, the method identifies the rational choice at every final decision node. When the analysis moves backward, a player’s previous threat is evaluated against the actual payoff structure at that moment. If the threatened action is not the maximizing choice at that subgame’s start, it is disregarded, or pruned, from the solution path .

Consider an incumbent firm threatening to start a costly price war if a new firm enters the market. If entry occurs, backward induction will reveal that the price war leads to losses for the incumbent, whereas accommodating the entrant yields a small but positive profit. Since the incumbent would rationally choose accommodation over the price war, the initial threat is non-credible and does not influence the entrant’s optimal decision, yielding a credible SPNE.

Summary

Utilizing the Extensive-Form Game Tree

• The Extensive-Form game is necessary for modeling interactions where players take turns sequentially.

• The structure uses a game tree to visually map the order of moves, starting from the initial node.

• Decision nodes indicate when a player acts, and the branches show the actions taken.

• The tree’s terminal nodes list the final payoffs, which depend on the path of moves taken.

The Subgame Perfect Nash Equilibrium (SPNE)

• The standard Nash Equilibrium is insufficient for sequential games as it can include irrational threats.

• The SPNE is a refined solution concept that demands strategies be optimal in the entire game and in every subgame.

• A subgame is any segment of the game tree beginning at a single decision node.

• The SPNE ensures that all actions are based on sequential rationality at every point in the game.

The Method of Backward Induction

• Backward induction is the primary technique used to computationally find the SPNE in sequential games.

• The process starts at the final decision nodes and identifies the maximizing choice for the player moving there.

• The analysis proceeds backward up the tree, with earlier players anticipating the rational choices of later players.

• This method guarantees that every player maximizes their expected payoff at every stage, resulting in a robust solution.

Eliminating Non-Credible Threats

• A key benefit of SPNE and backward induction is that they automatically remove strategies based on non-credible threats.

• A non-credible threat is an action proposed by a player that would be irrational (not payoff-maximizing) to carry out if the moment arrived.

• Backward induction reveals the optimal path, ignoring off-path threats that the threatening player would never execute.

• This ensures that the final predicted outcome is based only on credible and self-enforcing actions.

Apply backward induction to real-life negotiations.

• Identify the End Goal: Define the final, preferred outcome and payoff you wish to achieve in the negotiation.

• Map the Last Move: Determine the rational choice your counterpart will make right before the final agreement or collapse.

• Work Backwards: Based on the counterpart’s predicted final move, determine your best strategic move just prior to that.

• Establish the Opening Stance: Continue working backward to structure your opening offer or stance, ensuring all subsequent planned moves are optimal.

• Validate Credibility: Ensure any threats or promises you make are credible, meaning you would rationally carry them out if challenged.

Answer of the day

What is the primary solution method used to solve an Extensive-Form game tree?

Backward Induction.

Backward Induction is the required technique for solving sequential games represented by an Extensive-Form game tree. It involves starting at the final decision nodes and working backward toward the start of the game. By identifying the optimal choice at every stage, this method ensures the resulting strategy set is sequentially rational .

That’s A Wrap!

Want to take a break? You can unsubscribe anytime by clicking “unsubscribe” at the bottom of your email.